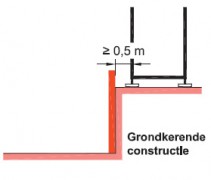
Zoals gezegd kan een 1e orde-berekening worden gemaakt zonder gebruik van PC en staafwerkprogramma. Bij een eenvoudige 1e orde-berekening wordt de draagkracht van de steigerconstructie getoetst door middel van een knikberekening. In deze paragraaf zijn rekenvoorbeelden opgenomen.
De voorspelling van het krachtenspel in de constructie is bij deze rekenmethode minder nauwkeurig dan bij een 2e orde-berekening. Dit komt omdat in een 1e orde-berekening niet alle factoren worden meegenomen die van invloed zijn op het statisch gedrag van de steigerconstructie. Bij een 1e orde-berekening wordt een eenvoudiger mechanicamodel gehanteerd, met uitgangspunten aan de conservatieve kant. Dit impliceert een grotere veiligheidsmarge in de berekening.
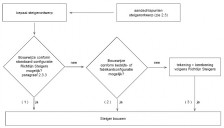
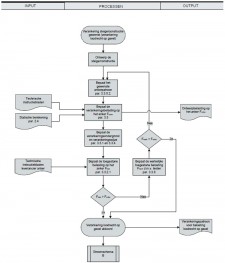
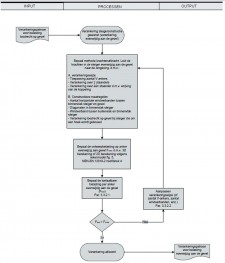
Daarom leidt een 1e orde-berekening in het algemeen tot een minder economisch ontwerp van de steigerconstructie vanwege meer materiaal en/of arbeid. Maar nogmaals: een 1e orde-berekening mag niet worden toegepast als deze mogelijkheid niet door het stroomschema volgens figuur 2.4.1¹ wordt geboden.
Enkele voorbeelden waarbij een eenvoudige 1e orde berekening niet is toegestaan:
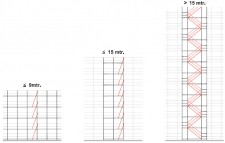
- steigers bekleed met netten met minder dan 50% doorlaatbaarheid
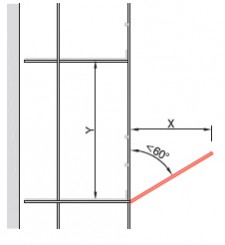
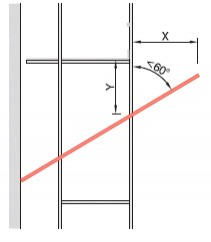
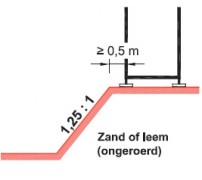
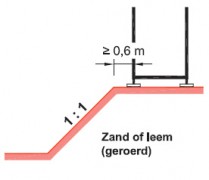
- steigers die op een hellend vlak staan (steiler dan 1:10)
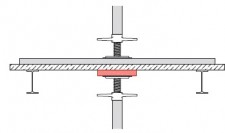
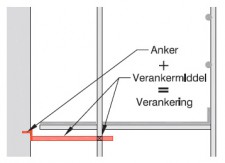
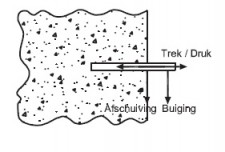
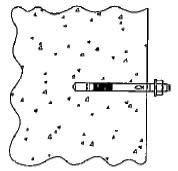
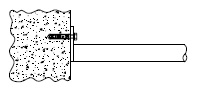
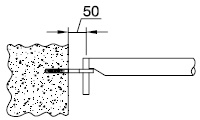
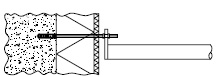
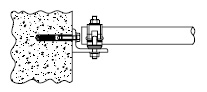
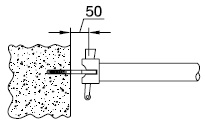
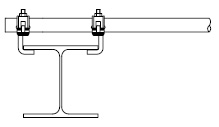
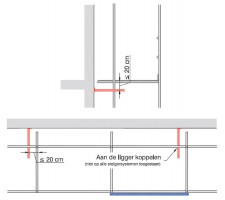
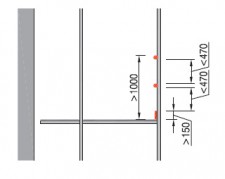
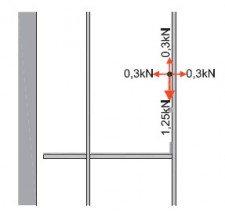
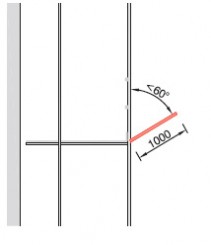
- indien op andere wijze dan door een uitbouwconsole of bekleding een extra moment in de staanders wordt geïntroduceerd, bijvoorbeeld als de verankering niet in de knooppunten is aangebracht
Er moet dan een 2e orde-berekening worden gemaakt.
Uitgangspunten
Bij 1e orde rekenen is het van belang om een vereenvoudigd mechanicamodel op te stellen waarbij:
- het rekenmodel onafhankelijk is van het beoogde steigertype
- de constructie wordt geschematiseerd als vakwerkconstructie (alleen normaalkrachten in staven)
- alle vlakken zijn geschoord of gesteund (zie voorwaarden geschoorde constructie, in deze paragraaf)
- alle opleggingen translatievast zijn
- er geen onderscheid is in het type verankering.
- knooppunten als scharnieren worden beschouwd
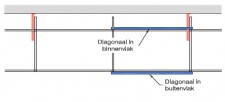
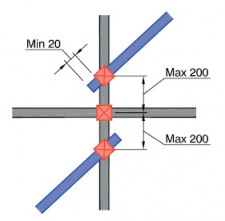
- diagonalen, verankeringen en/of afstempelingen aansluiten in de knooppunten
Voorwaarden geschoorde constructie
Ten aanzien van stabiliteit zijn er 3 typen steigerconstructies te onderscheiden:
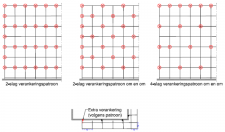
- Ongeschoorde steigers: steigers die niet of niet volledig geschoord zijn of waarbij de diagonalen niet in de knooppunten aangrijpen.
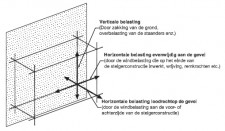
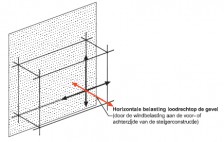
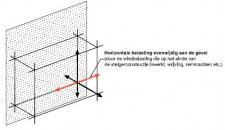
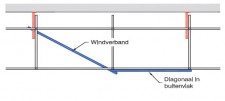
- Geschoorde steigers: steigers met volledige schoren die in de knooppunten aangrijpen. Elke bouwlaag (slag) van een steiger moet een volledige schoor bevatten om als geschoord te mogen worden beschouwd. Een volledige schoor is een schoor die er voor zorgt dat horizontale krachten uitsluitend via normaalkrachten naar de fundering worden overgedragen. Deze classificatie moet steeds per slag, per vlak en in iedere richting worden bekeken. Steigers kunnen geschoord worden met diagonalen.
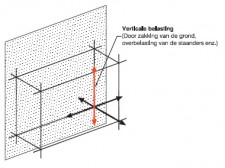
- Gesteunde steigers: steigers die hun stabiliteit ontlenen aan een andere constructie, bijvoorbeeld een gebouw of een stijf stalen raamwerk. De steungevende constructie moet ten minste 5 maal stijver zijn dan de gesteunde of “aanleunende” steiger (= vaak moeilijk te controleren). Steigers kunnen door middel van verankeringen en/of afstempelingen gesteund worden. Gesteunde steigers mogen ten aanzien van stabiliteit op dezelfde manier worden berekend als geschoorde steigers.
Een geschoorde of gesteunde constructie is stijf in ieder vlak. Daarom mag de inwendige stabiliteit worden gecontroleerd voor de onvervormde constructie. Dit noemen we een 1e orde berekening.
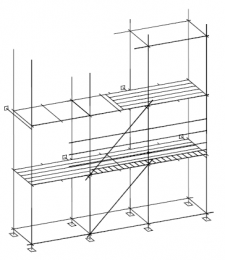
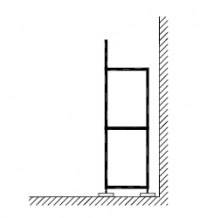
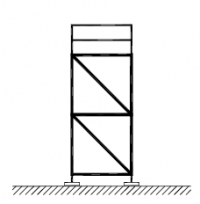
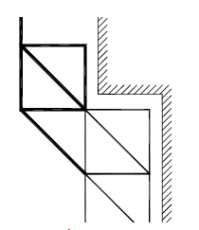
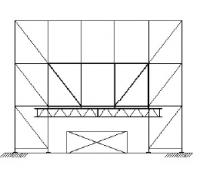
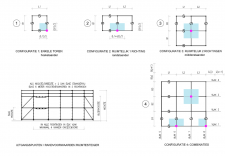
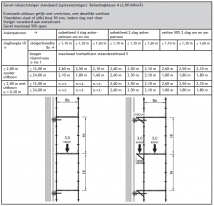
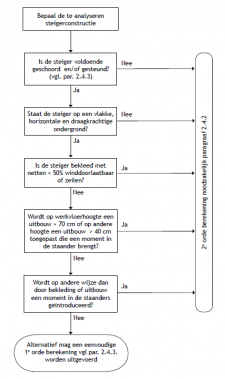
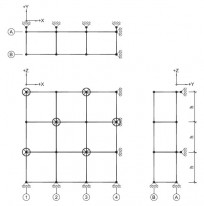
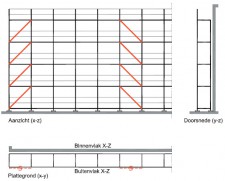
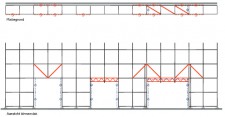
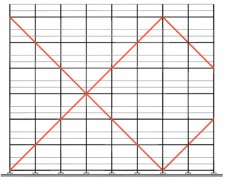
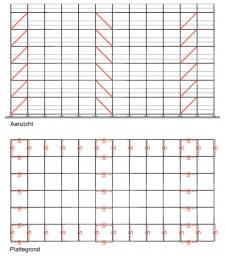
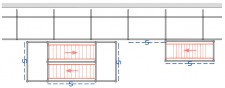
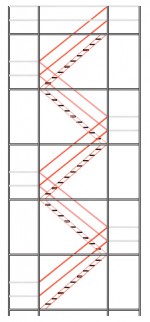
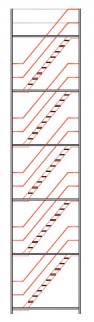
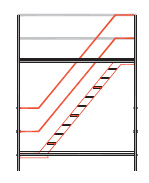
Figuren 2.4.31 tot en met 2.4.38 geven acht voorbeelden van geschoorde / gesteunde en ongeschoorde steigerconstructies, die al dan niet volgens een 1e orde berekening mogen worden getoetst. Tevens wordt hier aangegeven hoe de kniklengte kan worden bepaald.
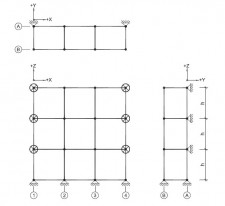
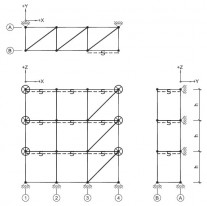
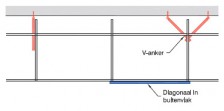
| Randvoorwaarden voor 1e orde rekenen (voorbeeld 1) | | Stramien | Vlak | Geschoord / gesteund | L-buc (kniklengte) | | 1 | Y-Z | Ja | l-buc = h | | 2 | Y-Z | Nee | Onbekend | | 3 | Y-Z | Nee | Onbekend | | 4 | Y-Z | Ja | l-buc = h | | A | X-Z | Ja | l-buc = h | | B | X-Z | Nee | Onbekend |
Figuur 2.4.3.1 Voorbeeld: toetsen volgens 1e orde berekening niet toegestaan |
Omdat niet voor alle vlakken wordt voldaan aan de randvoorwaarden mag deze configuratie niet met een 1e orde berekening worden getoetst.
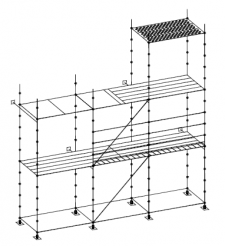
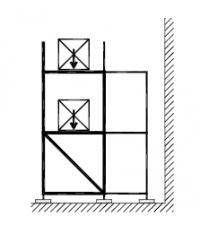
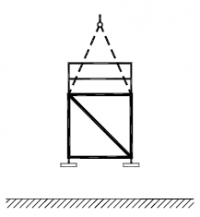
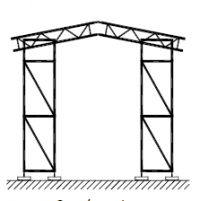
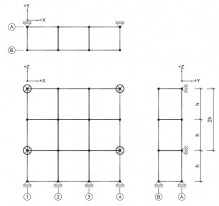
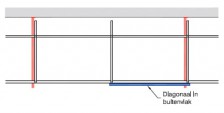
| Randvoorwaarden voor 1e orde rekenen (voorbeeld 2) | | Stramien | Vlak | Geschoord / gesteund | L-buc (kniklengte) | | 1 | Y-Z | Ja | l-buc = h | | 2 | Y-Z | Nee | Onbekend | | 3 | Y-Z | Nee | Onbekend | | 4 | Y-Z | Ja | l-buc = h | | A | X-Z | Ja | l-buc = h | | B | X-Z | Ja | l-buc = h |
Figuur 2.4.3.2 Voorbeeld: toetsen volgens 1e orde berekening niet toegestaan |
Omdat niet voor alle vlakken wordt voldaan aan de randvoorwaarden mag deze configuratie niet met een 1e orde berekening worden getoetst.
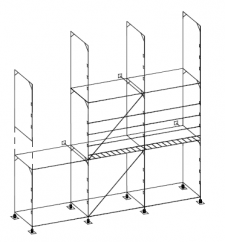
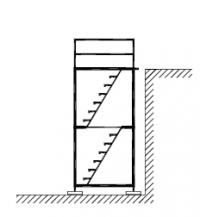
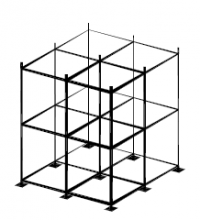
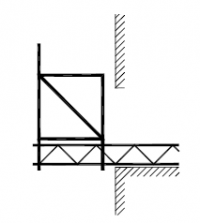
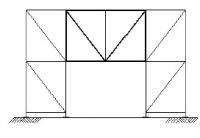
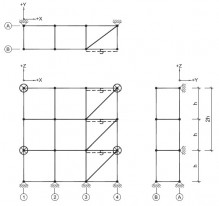
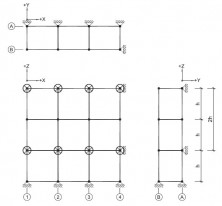
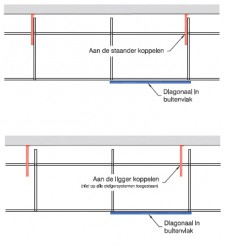
| Randvoorwaarden voor 1e orde rekenen (voorbeeld 3) | | Stramien | Vlak | Geschoord / gesteund | L-buc (kniklengte) | | 1 | Y-Z | Ja | l-buc = h | | 2 | Y-Z | Ja | l-buc = h | | 3 | Y-Z | Ja | l-buc = h | | 4 | Y-Z | Ja | l-buc = h | | A | X-Z | Ja | l-buc = h | | B | X-Z | Ja | l-buc = h |
Figuur 2.4.3.3 Voorbeeld: toetsen volgens 1e orde berekening toegestaan |
Omdat hier voor alle vlakken wordt voldaan aan de randvoorwaarden mag deze configuratie met een 1e orde berekening worden getoetst
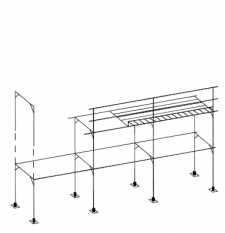
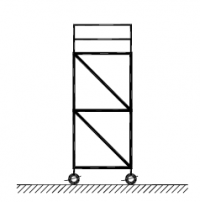
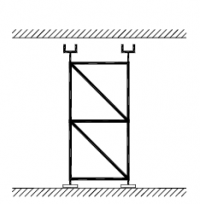
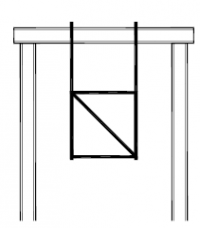
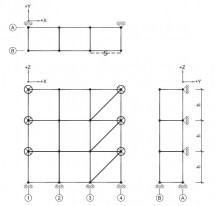
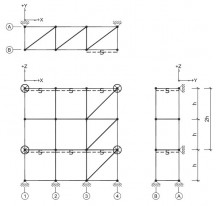
| Randvoorwaarden voor 1e orde rekenen (voorbeeld 4) | | Stramien | Vlak | Geschoord / gesteund | L-buc (kniklengte) | | 1 | Y-Z | Ja | l-buc = 2h | | 2 | Y-Z | Nee | Onbekend | | 3 | Y-Z | Nee | Onbekend | | 4 | Y-Z | Ja | l-buc = 2h | | A | X-Z | Ja | l-buc = 2h | | B | X-Z | Nee | Onbekend |
Figuur 2.4.3.4 Voorbeeld: toetsen volgens 1e orde berekening niet toegestaan |
Omdat niet voor alle vlakken wordt voldaan aan de randvoorwaarden mag deze configuratie niet met een 1e orde berekening worden getoetst.
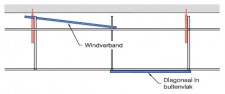
| Randvoorwaarden voor 1e orde rekenen (voorbeeld 5) | | Stramien | Vlak | Geschoord / gesteund | L-buc (kniklengte) | | 1 | Y-Z | Ja | l-buc = 2h | | 2 | Y-Z | Nee | Onbekend | | 3 | Y-Z | Ja | l-buc = 2h | | 4 | Y-Z | Ja | l-buc = 2h | | A | X-Z | Ja | l-buc = 2h | | B | X-Z | Ja | l-buc = 2h |
Figuur 2.4.3.5 Voorbeeld: toetsen volgens 1e orde berekening niet toegestaan |
Omdat niet voor alle vlakken wordt voldaan aan de randvoorwaarden mag deze configuratie niet met een 1e orde berekening worden getoetst.
| Randvoorwaarden voor 1e orde rekenen (voorbeeld 6) | | Stramien | Vlak | Geschoord / gesteund | L-buc (kniklengte) | | 1 | Y-Z | Ja | l-buc = 2h | | 2 | Y-Z | Ja | l-buc = 2h | | 3 | Y-Z | Ja | l-buc = 2h | | 4 | Y-Z | Ja | l-buc = 2h | | A | X-Z | Ja | l-buc = 2h | | B | X-Z | Ja | l-buc = 2h |
Figuur 2.4.3.6 Voorbeeld: toetsen volgens 1e orde berekening toegestaan |
Omdat hier voor alle vlakken wordt voldaan aan de randvoorwaarden mag deze configuratie met een 1e orde berekening worden getoetst.
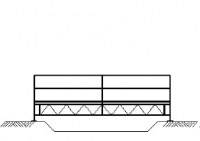
| Randvoorwaarden voor 1e orde rekenen (voorbeeld 7) | | Stramien | Vlak | Geschoord / gesteund | L-buc (kniklengte) | | 1 | Y-Z | Ja | l-buc = 2h | | 2 | Y-Z | Ja | l-buc = 2h | | 3 | Y-Z | Ja | l-buc = 2h | | 4 | Y-Z | Ja | l-buc = 2h | | A | X-Z | Ja | l-buc = 2h | | B | X-Z | Ja | l-buc = 2h |
Figuur 2.4.3.7 Voorbeeld: toetsen volgens 1e orde berekening toegestaan |
Omdat hier voor alle vlakken wordt voldaan aan de randvoorwaarden mag deze configuratie met een 1e orde berekening worden getoetst.
| Randvoorwaarden voor 1e orde rekenen (voorbeeld 8) | | Stramien | Vlak | Geschoord / gesteund | L-buc (kniklengte) | | 1 | Y-Z | Ja | l-buc = 2h | | 2 | Y-Z | Ja | l-buc = 2h | | 3 | Y-Z | Ja | l-buc = 2h | | 4 | Y-Z | Ja | l-buc = 2h | | A | X-Z | Ja | l-buc = 2h | | B | X-Z | Ja | l-buc = 2h |
Figuur 2.4.3.8 Voorbeeld: toetsen volgens 1e orde berekening toegestaan |
Omdat hier voor alle vlakken wordt voldaan aan de randvoorwaarden mag deze configuratie met een 1e orde berekening worden getoetst.
Rekenwijze
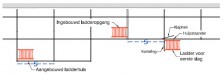
Bij een 1e orde berekening kan de toelaatbare knikkracht in de staander worden bepaald, dmv een standaard knikberekening. De toegestane knikkracht voor standaard steigerbuis is in Rekenvoorbeeld 1 berekend. Figuur 2.4.39 toont voor een aantal kniklengten de toegestane knikkracht. Afhankelijk van de situatie en/of bouwvorm moeten op deze knikkrachten nog reductiefactoren worden toegepast.
| Kniklengte λy;buc | Slankheid λy | Slankheid λy;rel | ω y;buc | Knikkracht N c;s;d |
| 1000 mm | 63 | 0,67 | 0,8008 | 80,3 kN |
| 2000 mm | 125 | 1,33 | 0,4088 | 39,5 kN |
| 3000 mm | 188 | 2,00 | 0,2081 | 20,1 kN |
| 4000 mm | 250 | 2,66 | 0,1231 | 11,9 kN |
Figuur 2.4.39 Toegestane knikkracht (designwaarde) in de staander
als functie van de kniklengte |
Reductiefactor wind
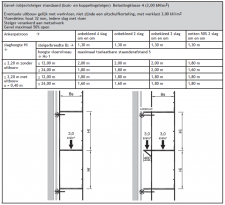
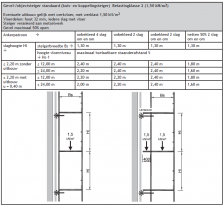
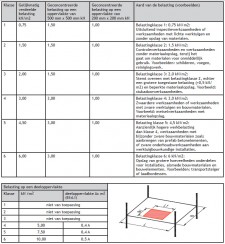
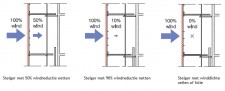
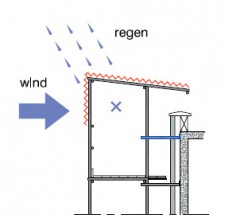
Voor steigers die buiten staan (en dus onderhevig zijn aan windbelasting) moet op de toegestane knikkracht een reductiefactor volgens figuur 2.4.310 worden toegepast. Dit als compensatie voor de verminderde draagkracht van de staander als gevolg van wind.
| Reductiefactor knikkracht staander t.g.v. windbelasting | Onbekleed | Bekleed met netten > 50% doorlaatbaar |
| Kniklengte [m] | Knikkracht [kN] | Staanderafstand
≤ 1,80 m | Staanderafstand
> 1,80 m | Staanderafstand
≤ 1,80 m | Staanderafstand
> 1,80 m |
| 1 | 80,3 | 0,95 |
| 2 | 39,5 | 0,8 |
| 3 | 20,1 | 0,8 | 0,7 | 0,7 | 0,5 |
| 4 | 11,9 | 0,6 | 0,4 | 0,4 | 0,0 |
| Figuur 2.4.310 Reductiefactor knikkracht staander als gevolg van windbelasting |
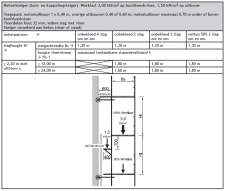
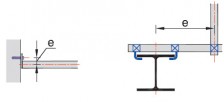
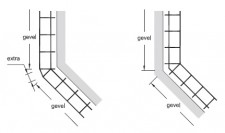
Reductiefactor uitbouw
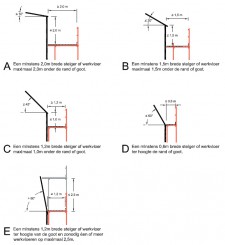
Wordt een uitbouw toegepast, dan moet er een reductiefactor volgens figuur 2.4.311 worden toegepast. Dit om het daardoor in de staander ontstane extra moment mee te nemen.
| Reductiefactor knikkracht staander t.g.v. uitbouwconsole | Uitbouw ≤ 40 cm | Uitbouw ≤ 70 cm |
| Kniklengte [m] | Knikkracht [kN] | Staanderafstand
≤ 1,80 m | Staanderafstand
> 1,80 m | Staanderafstand
≤ 1,80 m | Staanderafstand
> 1,80 m |
| 1 | 80,3 | 0,8 | 0,7 | 0,5 | 0,3 |
| 2 | 39,5 |
| 3 | 20,1 |
| 4 | 11,9 |
| 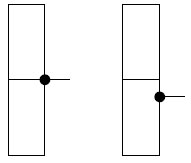
Uitbouw < 40 cm | 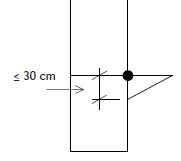
≤ 30 cm Uitbouw < 70 cm |
| Figuur 2.4.311 Reductiefactor knikkracht staander als gevolg van uitbouwconsole |
Alternatief
In plaats van het gebruik van deze conservatieve reductiefactoren mag ook een “berekening met de hand” worden uitgevoerd overeenkomstig TGB (NEN 6770:1997). Vanzelfsprekend dienen hierbij de randvoorwaarden volgens de rekenregels van paragraaf 2.4 te worden gehanteerd. Zie Rekenvoorbeeld 2.
Toets draagkracht verankeringen
De draagkracht van de verankeringen moet separaat worden getoetst. Zie hiervoor paragraaf 3.3.
| Rekenvoorbeeld 1 – 1e orde berekening (met behulp van tabellen uit paragraaf 4.3) Staanderbelasting |
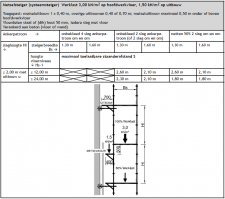
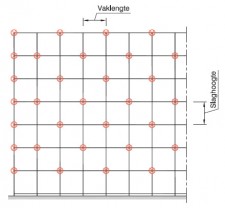
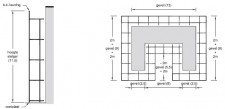
We gaan er in dit voorbeeld van uit dat de steigers in de figuren 2.4.31 t/m 2.4.38 zijn voorzien van 2 houten werkvloeren (op respectievelijk 2 m+ en 4 m+), met een kantplank en dubbele leuning (niet getekend). Slaghoogte bedraagt 2 m, vaklengte 2 m, breedte 1,5 m. Steiger conform belastingklasse 4: 3,00 kN/m²
Dan gelden voor een gevelsteiger conform figuur 2.4.33 voor staander A-3 de waarden genoemd in figuur 2.4.312.In dit voorbeeld wordt aan de binnenstaander een uitbouw van 30 cm gerekend, met een nuttige belasting van 3,00 kN/m². Voor staander B2 in figuur 2.4.37 gelden de waarden genoemd in figuur 2.4.313. |
| Omschrijving | | lengte (m) | | breedte / (m) | | aantal (%) | | aantal (st) | | gewicht | | | eigen gewicht | | nuttige |
| | | | | | | | | belasting |
| Staanders | : | 6 | x | 1 | x | 100 % | x | 1 | x | 50 | N/m | = | 300 | N | |
| Liggers 2 m | : | 2 | x | 2 | x | 50 % | x | 3 | x | 50 | N/m | = | 300 | N | |
| Liggers 1,5 m | : | 1,5 | x | 1 | x | 50 % | x | 3 | x | 50 | N/m | = | 113 | N | |
| Hor. diagonaal | : | 2,5 | x | 1 | x | 50 % | x | 3 | x | 50 | N/m | = | 188 | N | |
| Kortelingen | : | 1,5 | x | 2 | x | 50 % | x | 2 | x | 50 | N/m | = | 150 | N | |
| Vloer | : | 2 | x | 1,5 | x | 50 % | x | 2 | x | 300 | N/m² | = | 900 | N | |
| Uitbouw | : | 2 | x | 0,3 | x | 100 % | x | 2 | x | 300 | N/m² | = | 360 | N | |
| | | | | | | | | | | | | | | | |
| Vloerbelasting | : | 2 | x | 1,5 | x | 50 % | x | 1,5 | x | 3000 | N/m² | = | | | 6750 N |
| Uitbouw | : | 2 | x | 0,3 | x | 100 % | x | 1,5 | x | 3000 | N/m² | = | | | 2700 N |
| | | | | | | | | | | | | | ——— | | ——– |
| | | | | | | | | | | | | | 2310 | N | 9450 N |
| |
| | | | | | | | | | | | | | 2,3 | kN | 9,45 kN |
| Belastingfactoren | | | | | | | | | | | 1,2 | x | 1,5 x |
| | | | | | | | | | | | | | 2,8 | | 14,2 |
| | | | | | | | | | | | | | | | |
| Totaal | : | | | | | | | | | Fb3;d | | = | 17,0 | kN | |
| | | | | | | | | | | | | | | | |
Figuur 2.4.312 Rekenvoorbeeld voor staander A3 in figuur 2.4.33
Noot: Bij verwijzing naar TGB normen mogen vergelijkbare Eurocodes toepast worden, zolang een vergelijkbaar veiligheidsniveau gehandhaafd blijft.
| Omschrijving | | lengte (m) | | breedte / (m) | | aantal (%) | | aantal (st) | | gewicht | | | eigen gewicht | | nuttige |
| | | | | | | | | belasting |
| Staanders | : | 6 | x | 1 | x | 100 % | x | 1 | x | 50 | N/m | = | 300 | N | |
| Liggers 2 m | : | 2 | x | 2 | x | 50 % | x | 3 | x | 50 | N/m | = | 300 | N | |
| Liggers 1,5 m | : | 1,5 | x | 1 | x | 50 % | x | 3 | x | 50 | N/m | = | 113 | N | |
| Leuning 2 m | : | 2 | x | 2 | x | 100 % | x | 2 | x | 50 | N/m | = | 400 | N | |
| Kantplank | : | 2 | x | 1 | x | 100 % | x | 2 | x | 60 | N/m | = | 240 | N | |
| Kortelingen | : | 1,5 | x | 2 | x | 50 % | x | 2 | x | 50 | N/m² | = | 150 | N | |
| Vloer | : | 2 | x | 1,5 | x | 50 % | x | 2 | x | 300 | N/m² | = | 900 | N | |
| | | | | | | | | | | | | | | | |
| Vloerbelasting | : | 2 | x | 1,5 | x | 50 % | x | 1,5 | x | 3000 | N/m² | = | | | 6750 N |
| | | | | | | | | | | | | | ——— | | ——– |
| | | | | | | | | | | | | | 2403 | N | 6750 N |
| |
| | | | | | | | | | | | | | 2,4 | kN | 6,8 kN |
| Belastingfactoren | | | | | | | | | | | 1,2 | x | 1,5 x |
| | | | | | | | | | | | | | 2,9 | | 10,1 |
| | | | | | | | | | | | | | | | |
| Totaal | : | | | | | | | | | Fb3;d | | = | 13,0 | kN | |
| | | | | | | | | | | | | | | | |
Figuur 2.4.313 Rekenvoorbeeld voor staander B2 in figuur 2.4.37
Knikkracht staanders
Doorsnede-eigenschappen:
Buis Φ 48,3 x 3,2 mm
A = 453 mm²
Wx;el = 4800 mm³
Wx;pl = 6520 mm³ | S235JRG2 | fy;rep = 235 N/mm² | NEN-EN 39 |
Controle knik in gedrukte buis (volgens NEN 6770, hoofdstuk 12).
Voor slaghoogte 2 m geldt:
- Slankheid λy = ly;buc / iy = 2000 mm / 16 mm = 125
- Voor steigerbuis geldt: fy;d = 235 N/mm2.
- Eulerse slankheid λe = π x √(Ed / fy;d) = 3,14 x √(2,1 x 105 / 235) = 94
- Relatieve slankheid λy;rel = λy / λe = 125 / 94 = 1,33
- Uit instabiliteitskromme b volgt: (NEN 6770, tabel 24) knikfactor: ωy;buc = 0,4088
- Nc;u;d = A x fy;d / γM (NEN 6770, 11.2.2) = 453 mm2 x 235 N/mm2 = 106455 N / 1,1 = 96,7 kN
Designwaarde knikkracht = Nc;u;d x ωy;buc = 96,7 x 0,4088 = 39,5 kN
Op vergelijkbare wijze is de knikkracht bepaald bij andere staanderlengtes (zie figuur 2.4.39).
Toetsing staanderbelastingen
| Staander | Fu;d | knik-lengte | design knikkracht volgens tabel 2.4.39 | reductie wind
volgens tabel 2.4.310 | reductie uitbouw volgens tabel 2.4.311 | | Fu;d;red | Toetsing |
| 2.4.33-A3 | 17,0 kN | 2 m | 39,5 kN | x 0,8 | x 0,7 | = | 22,1 kN | Voldoet |
| 2.4.37-B2 | 13,0 kN | 4 m | 11,9 kN | x 0,4 | – | = | 4,8 kN | Voldoet niet |
Figuur 2.4.314 Toetsing staanderbelastingen
Genoemde staanders zijn maatgevend, de overige staanders worden even zwaar of minder belast.
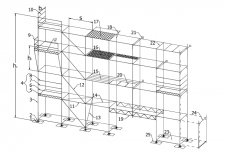
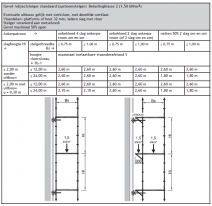
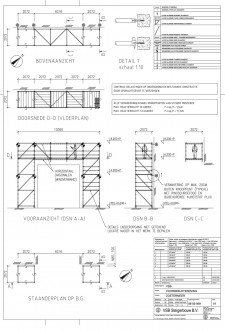
| Rekenvoorbeeld 2 – 1e orde berekening (met behulp van NEN 6770) |
|
Figuur 2.4.315 Rekenvoorbeeld 2: 1e orde berekening met behulp van NEN 6770